Linearized and Single-Pass Belief Propagation
Wolfgang Gatterbauer, Stephan Günnemann, Danai Koutra, Christos FaloutsosCarnegie Mellon University, 2015
Task
Homophily vs Heterophily
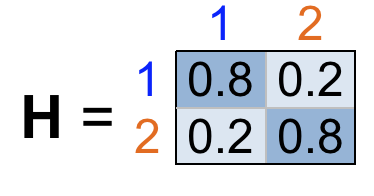
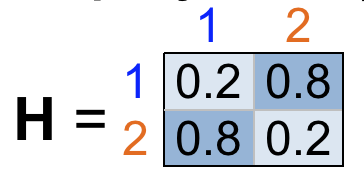
Label Propagation with Affinity Matrix
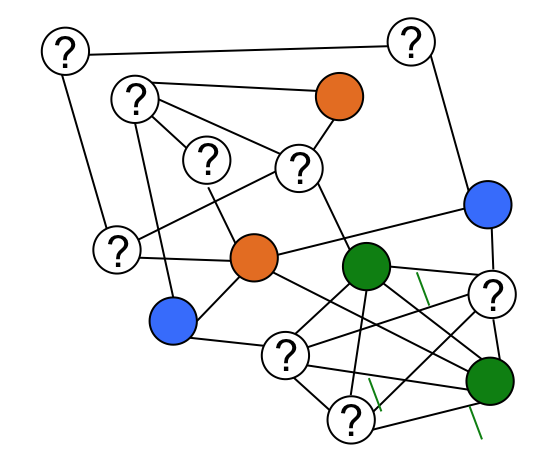

Setting
Belief Propagation
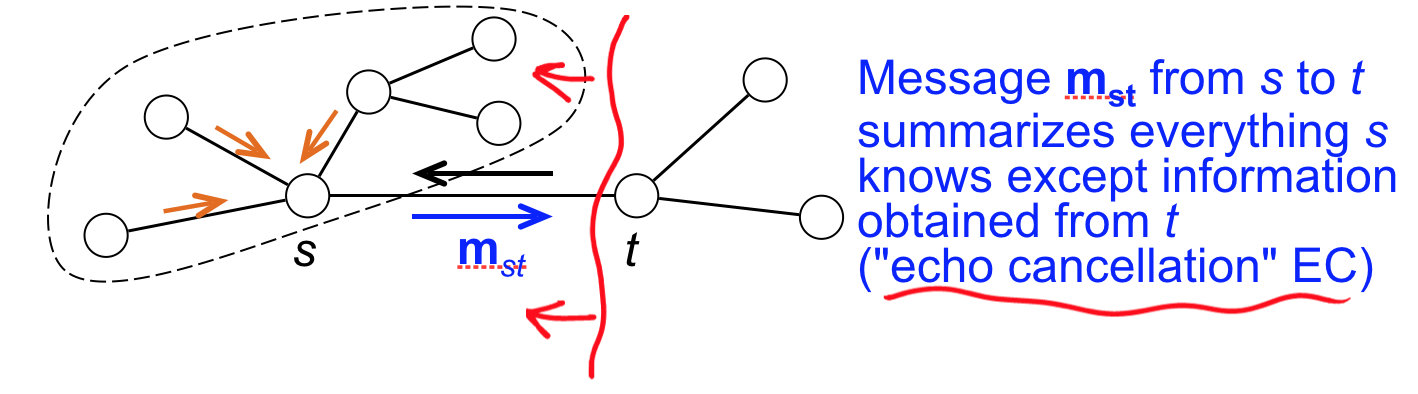
Bad News 😭
- CONVERGENCE is not guaranteed: especially with loopy graphs.
- The original authors don't even assure its correctness as an approximation algorithm.
Linearized Belief Propagation (LinBP)
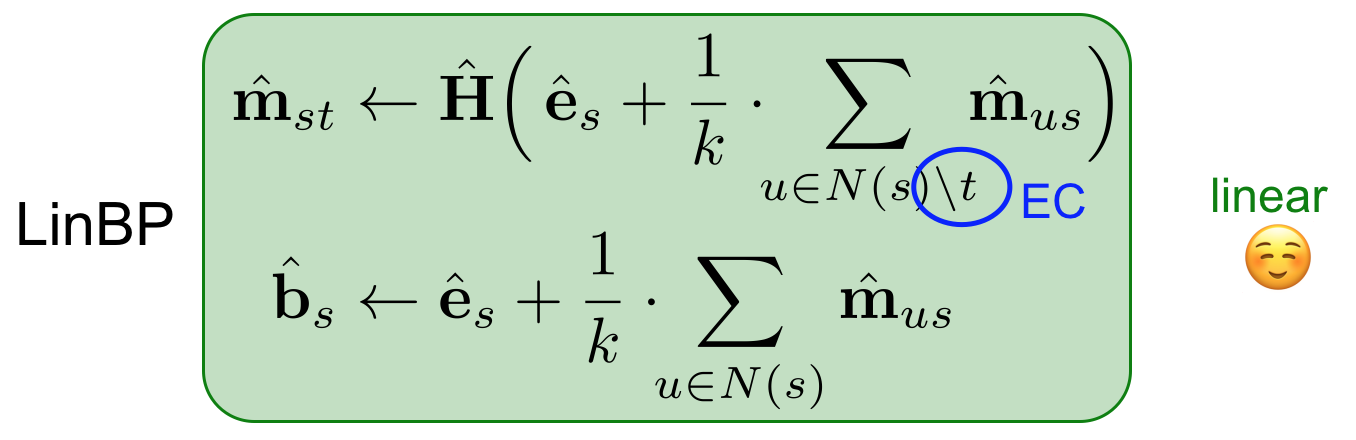
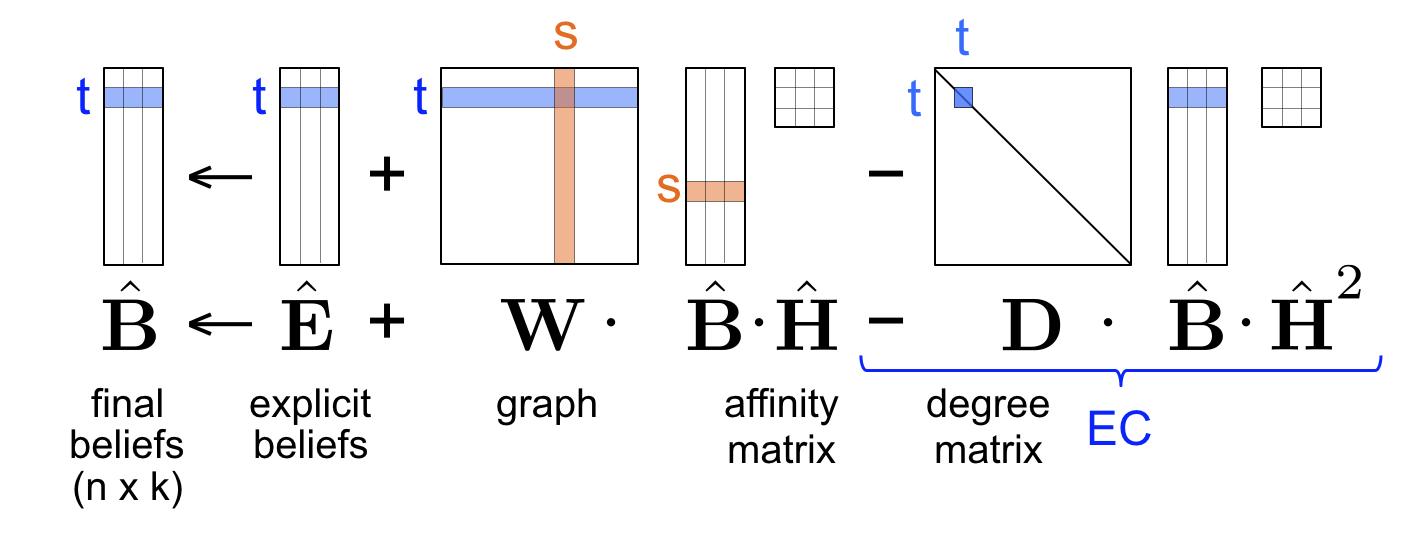
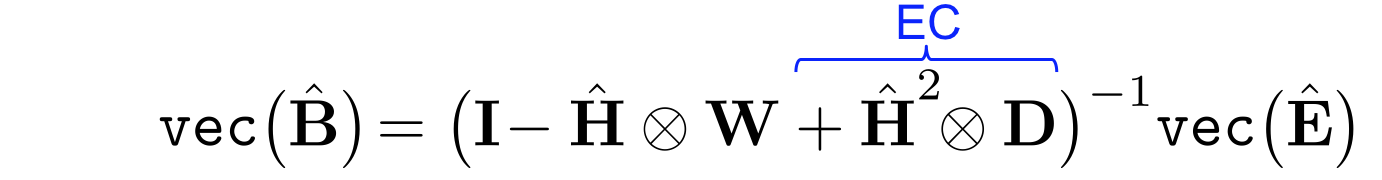
LinBP implementation in SQL
(yes, SQL)
Good News 😎: CONVERGENCE!
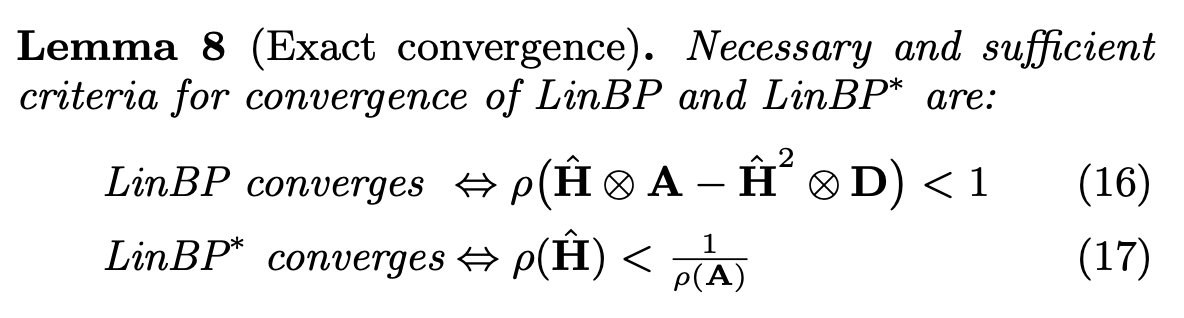

Single-Pass Belief Propagation (SBP)
Generalities
- The authors define a modified BP algorithm that calculates the final beliefs in at most one step.
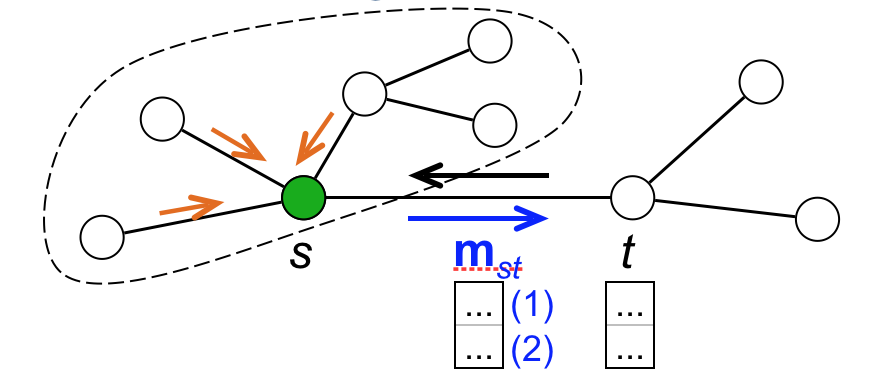
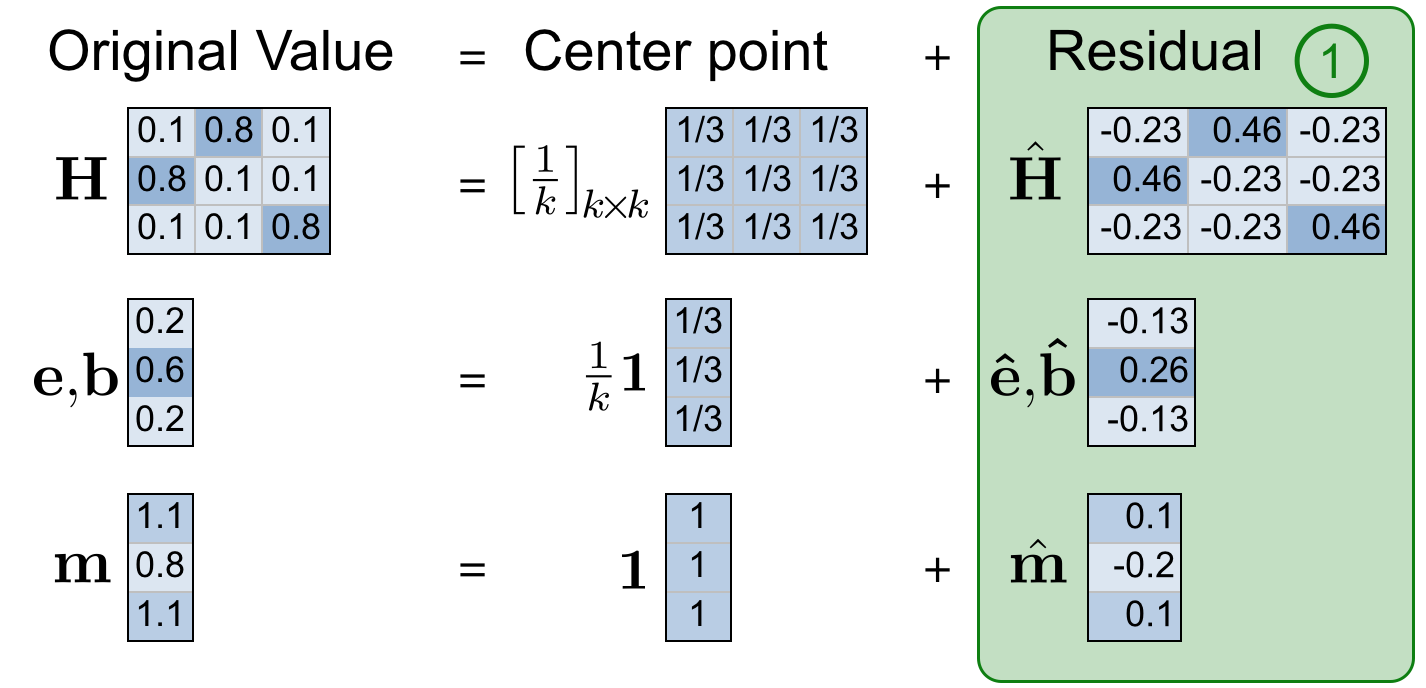
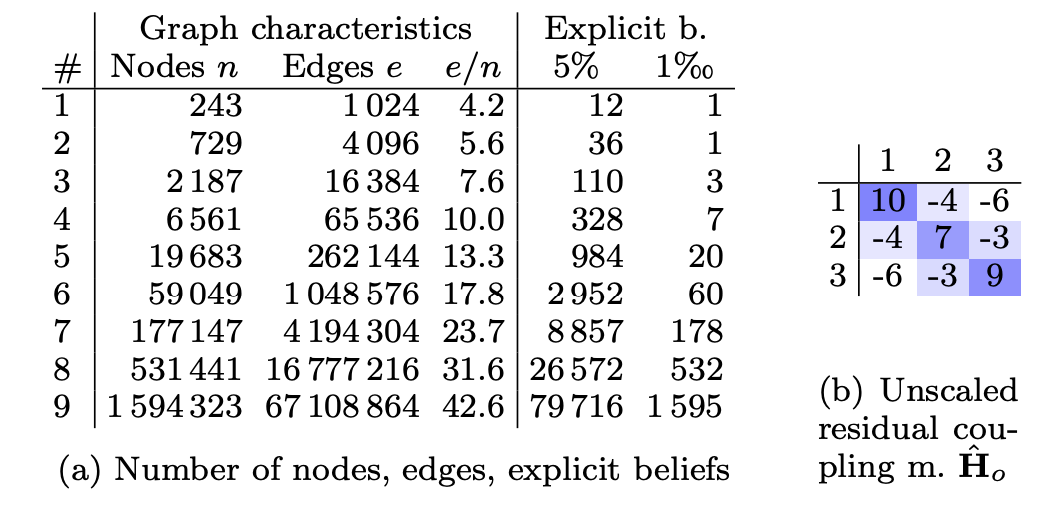
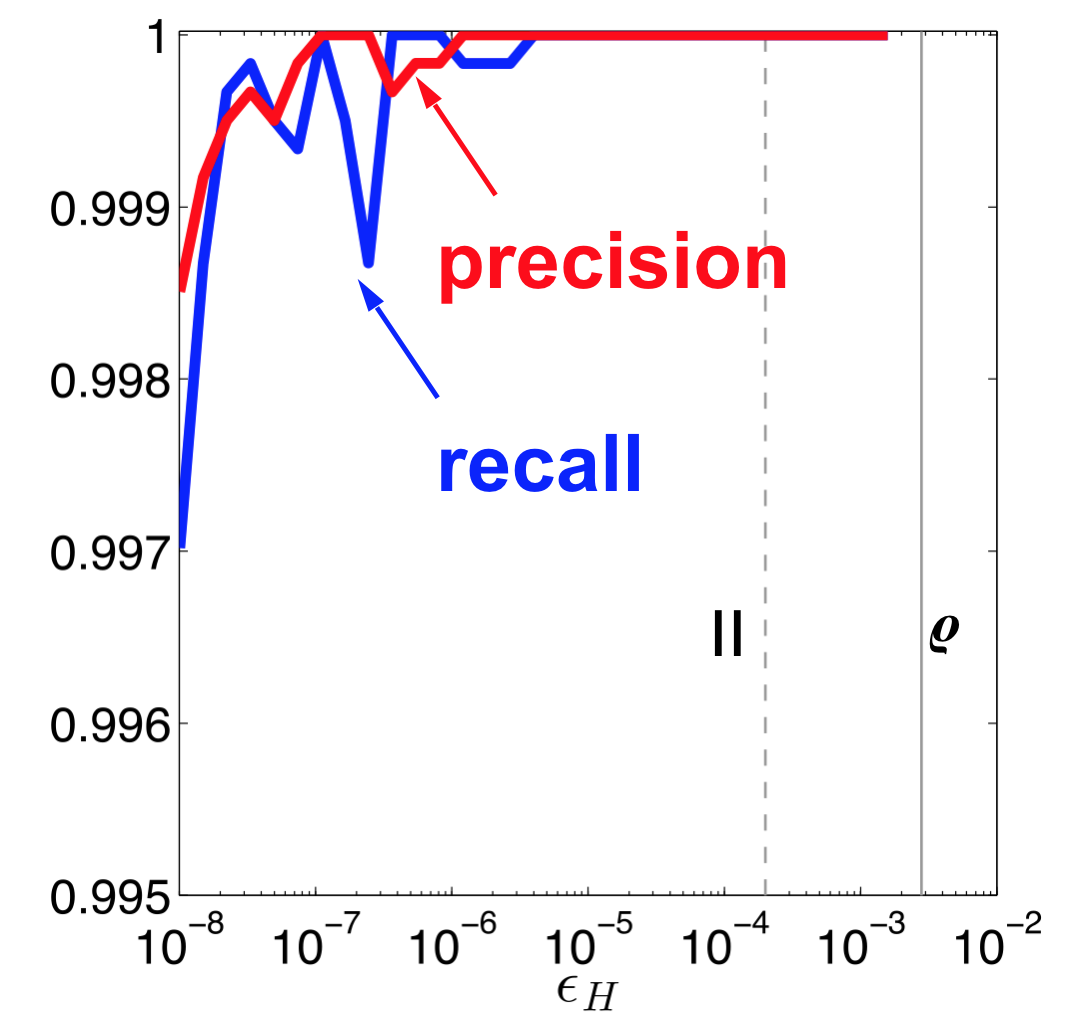
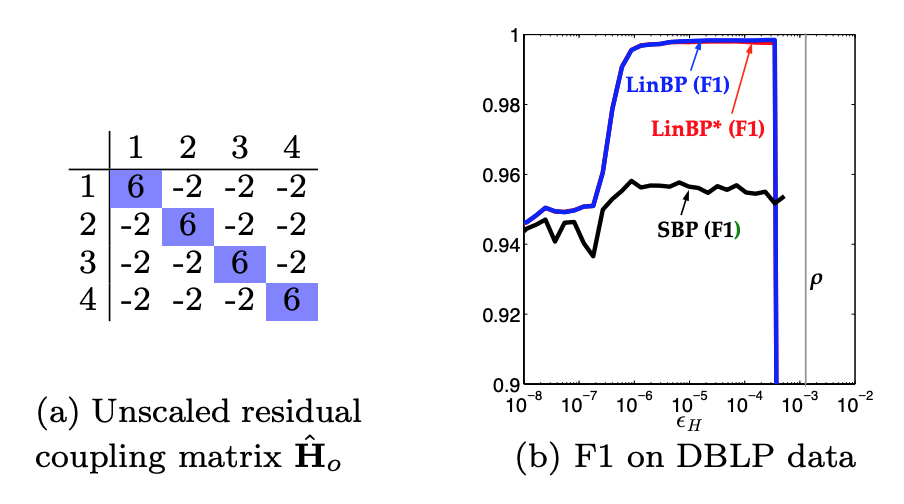
- Consider the residual (from LinBP) coupling matrix. Call it now $\hat{\mathbf{H}}_0$. Now we define a scaled matrix $\hat{\mathbf{H}} := \epsilon_H \hat{\mathbf{H}}_0$. This scaling factor $\epsilon_H$ helps to justify the correctness of SBP.
Generalities
- As $\lim_{\epsilon_H \to 0}$, SBP's predictions converge to those from LinBP.
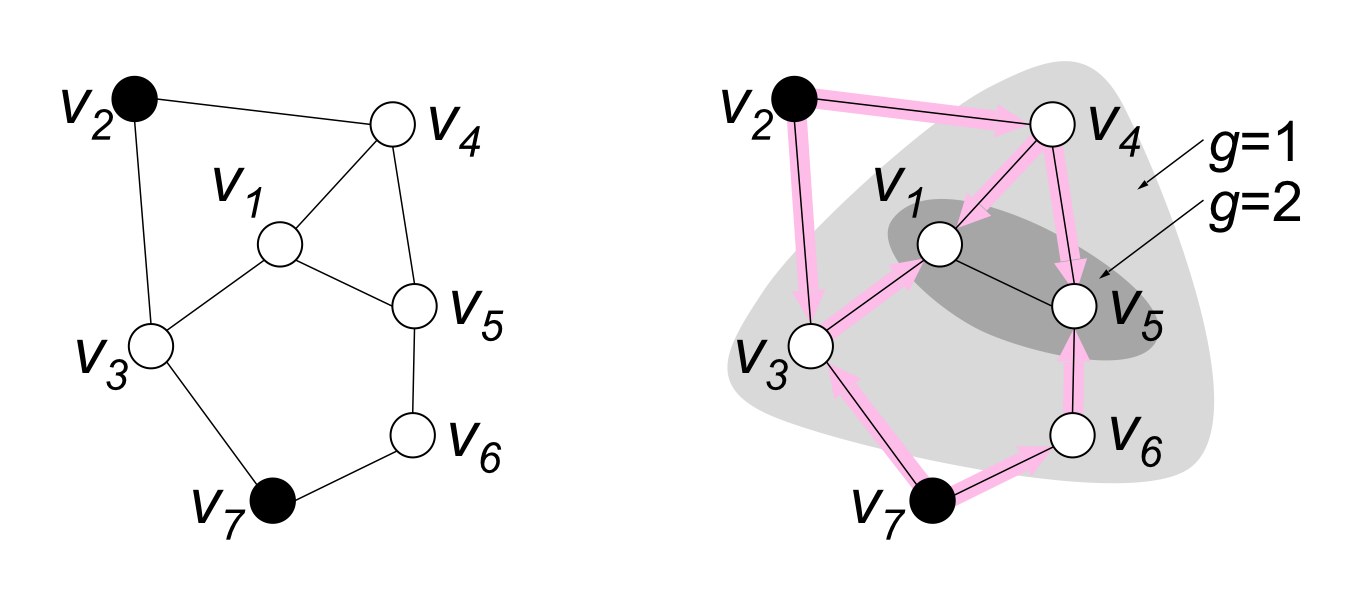
- (Geodesic number g): given a node $t$, its geodesic number $g_t$ is defined as the length of the shortest path to any node with explicit beliefs.
- Main idea: the influence a node affects other nodes increases with less distance between.
SBP Equation
Given node $t$ and geodesic number $k$, we define$$\hat{\mathbf{b}}_t = \hat{\mathbf{H}}^k \sum_{p \in P_t^k} w_p\hat{\mathbf{e}}_p$$
where
- $p_t^k$ is the set of all paths with length $k$ from a node with explicit beliefs to $t$,
- $w_p$ is the weight of any path $p \in p_t^k$,
- $\hat{\mathbf{e}}_p$ are the explicit beliefs of the node at the start of path $p$.
How geodesic numbers take part of belief propagation
Experiments
Datasets
- Synthetic: The authors created 9 "Kronecker graphs" of varying sizes ans picked 5% nodes randomly to assignthem two classes ($k=2$) in the range $[-0.1, 0.1]$.
- Real: DBPL data was used, consisting of 36 138 nodes representing papers, authors, converences, and terms ($k=4$).
Kronecker Dataset
Great Accuracy (LinBP vs BP)
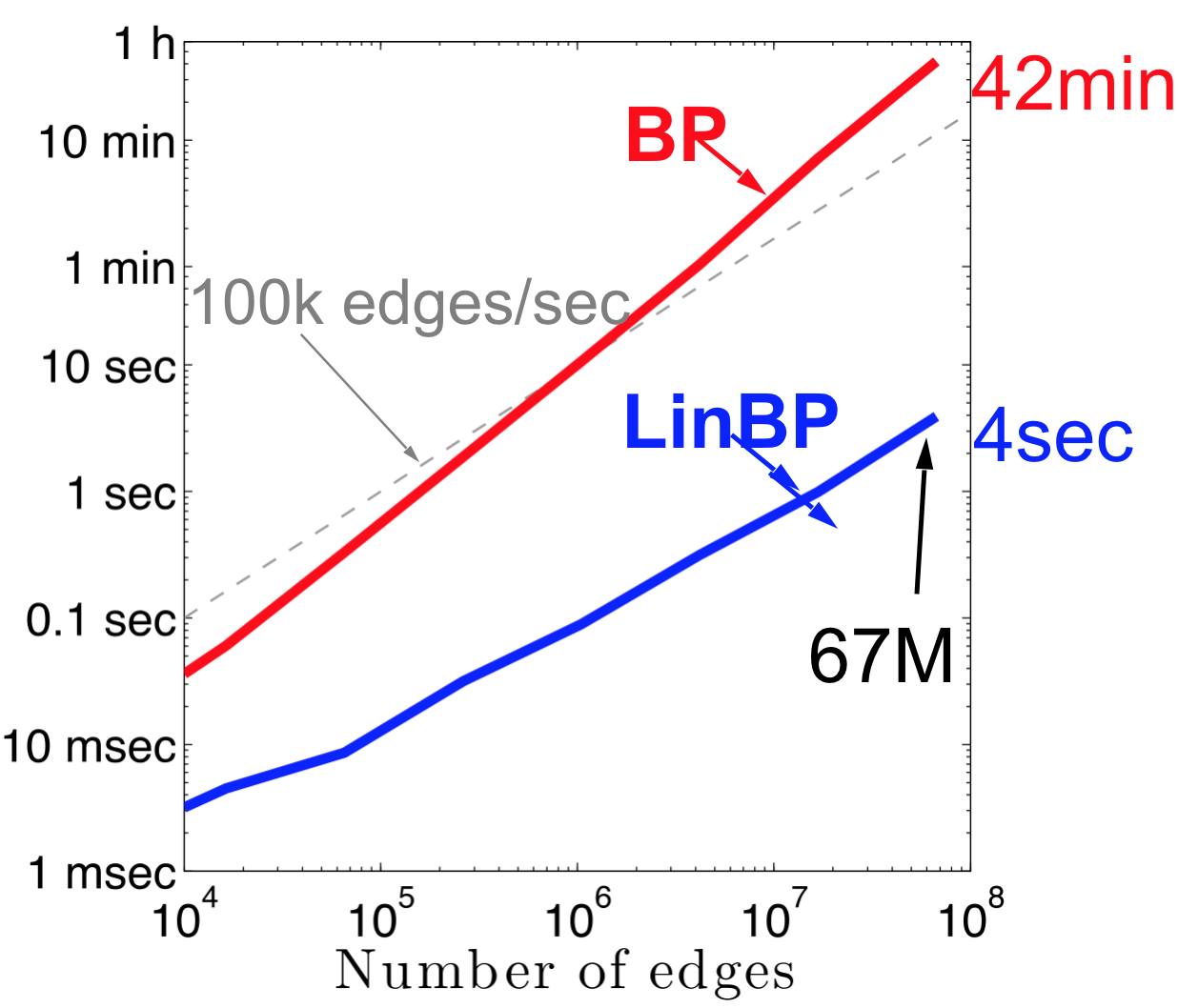
Great Scalability (LinBP vs BP)
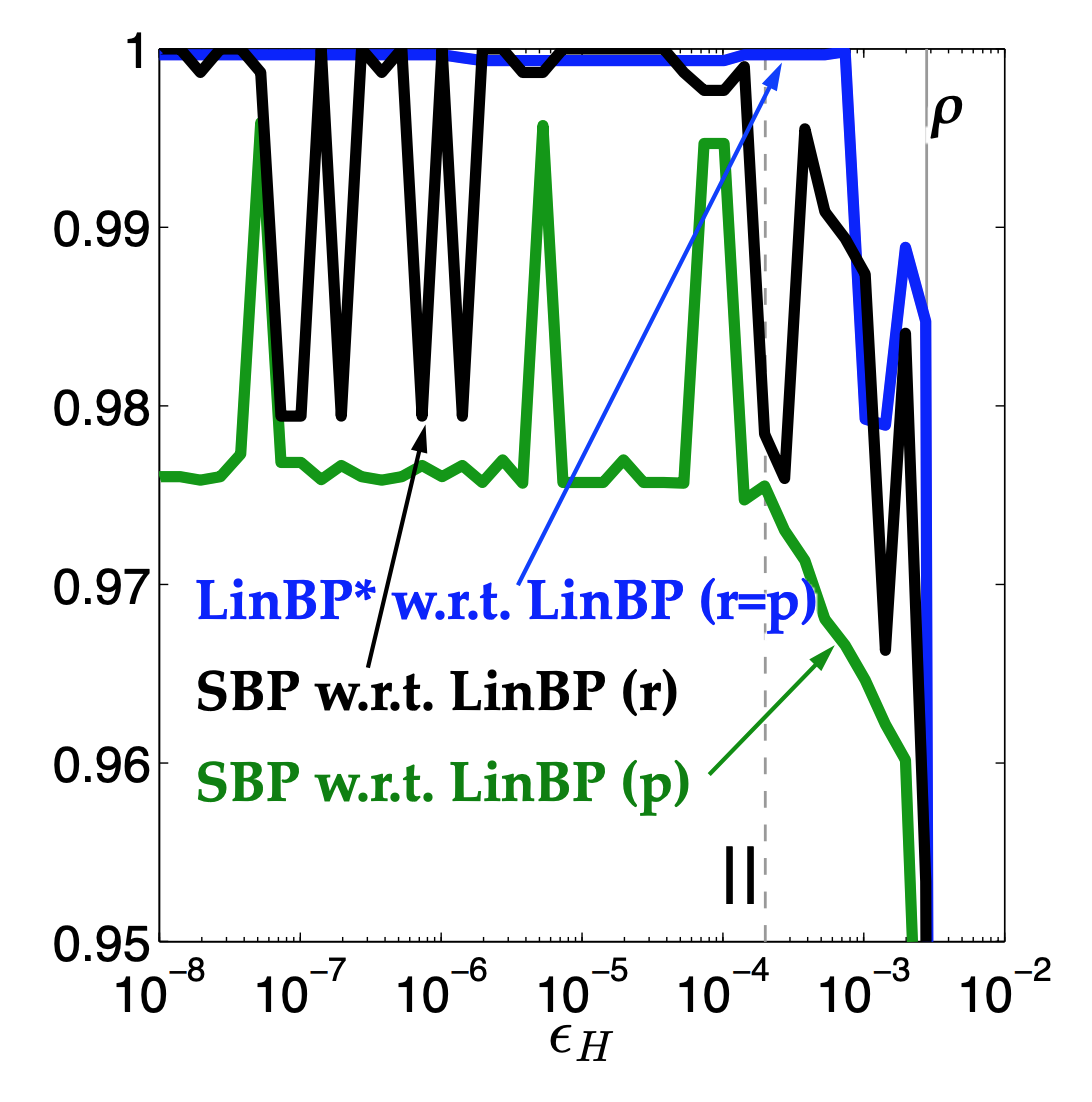
LinBP vs LinBP* vs SBP
DBPL Results
Summary of Results
The main memory implementation of LinBP is up to 600 times faster than BP, and the SQL implementation of SBP is more than 10 times faster than LinBP.
SBP needs fewer iterations to converge and requires fewer calculations for each iteration, on average.
In the experiments, it was faster to update SBP when less than $\approx$ 50% of the final explicit beliefs are new.
BP, LinBP, LinBP$^∗$, and SBP give almost identical top belief assignments (depending on $\epsilon_H$). However, ties can drop the quality of SBP to $\leq$ 95%.
Conclusions
Goal: propagate multi-class heterophily from labels
Problem: How to solve BP convergence issues ☹
Solution: Center & linearize BP ⇒ convergence & speed 🙂
Linearized Belief Propagation (LinBP): Matrix Algebra, convergence, closed-form SQL (w/ recursion) with standard aggregates
Single-pass Belief Propagation (SBP) Myopic version, incremental updates