Adversarial Perturbations of Opinion Dynamics in Networks
Jason Gaitonde, Jon Kleinberg, Éva TardosCornell University
2020
presented by Albert M Orozco Camacho
Motivation
Opinion dynamics has been previously studied within the mathematical social sciences literature; yet not much attention has been put to current social network studies.
On the other hand, perturbations that induce discord in social media are of important interest for current research in politics, sociology, economics, computer science, etc.
Adversarial Attacks to Induce Discord
The authors present a formal study on the intuition that a (maliscious) actor attacks the overall opinion consensus of a network.
These perturbations will difuse via an opinion dynamics model.
Problem
An adversarial agent targets a few individual opinions to difuse a sense of discord.
Task
Identify the most vulverable structures within a network. Mitigate these attacks by insulating nodes.
Convex Optimization
Definitions
Matrices
Adjacency Matrix $$A_{i,j} = A_{j,i} := w(i,j)$$Diagonal Matrix $$D_{i,i} = \sum_{j \in V} w(i,j)$$
Laplacian Matrix $$L := D - A$$
Some Spectral Properties
$$ \mathbf{x}^T L \mathbf{x} = \sum_{(i,j) \in E} w(i,j)(\mathbf{x}(i)-\mathbf{x}(j))^2 $$
$$ L = \sum_{i=1}^n \lambda_i\mathbf{v}_i\mathbf{v}_i^T $$
Friedkin-Johnsen Dynamics
Given $G = (V, E, w)$ and an initial opinion vector $s \in \mathbb{R}^n$.Start with $\mathbf{z}^{(0)} = \mathbf{s}$.
For each node $i \in V$, update $$ \mathbf{z}^{(t+1)}(i) = \frac{\mathbf{s}(i) + \sum_{j \in V} w(i,j)\mathbf{z}^{(T)}(j)} {1 + \sum_{j \in V} w(i,j)} $$
Friedkin-Johnsen Dynamics
Convergence will be reached and the limiting final opinion vector is given by $$\mathbf{z} = (I + L)^{-1}\mathbf{s}$$
Adversarial Optimization
General Formulation
$$
\max_{s \in \mathbb{R}^n: ||\mathbf{s}||_2 \leq R}
\mathbf{s}^T (I + L)^{-1}f(L)(I + L)^{-1}\mathbf{s}
$$
where $f: \mathbb{R} \to \mathbb{R}$ satisfies $f(y) \geq 0$ for $y \geq 0$
The adversary will first supply initial opinions $\mathbf{s}$ (e.g. via fake news)
The opinions become diffused via the Friedkin-Johnsen dynamics
The goal of the adversary is to choose these initial opinions in order to maximally induce some desired effect
Disagreement
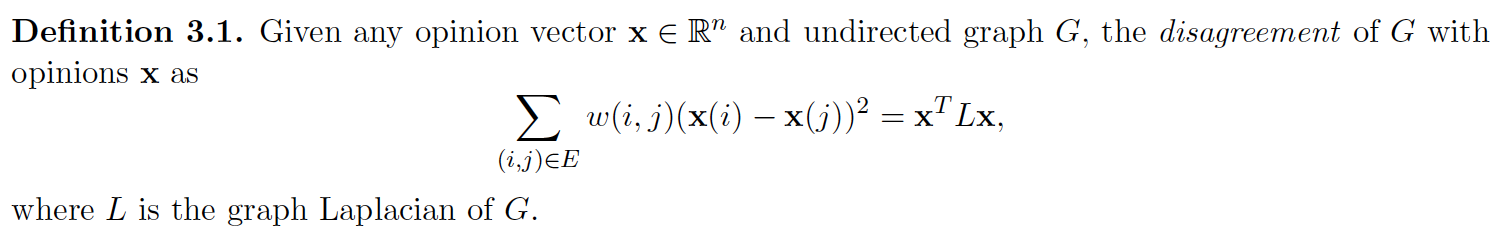
Polarization of $\mathbf{x}$: $$||\bar{\mathbf{x}}||_2^2 = \sum_{i=1}^n \bar{\mathbf{x}}(i)^2$$
Optimizing Disagreement
Let $f(y) = y$. Maximizing disagreement yields the objective
$$
\max_{s \in \mathbb{R}^n: ||\mathbf{s}||_2 \leq R}
\mathbf{s}^T (I + L)^{-1}L(I + L)^{-1}\mathbf{s}
$$
$L$ both dictates the measurement of disagreement, and the opinion dynamics themselves
When each individual is not listening to their neighbors (very sparse graph)
The adversary's strategy is to simply feed in opinions that directly maximize disagreement in $G$, as the opinion dynamics are negligible
As connectivity gets stronger, the optimizer is proportional to the second largest nonzero eigenvalue (namely, $\lambda_2$)
In this case, the initial opinion vector inducing maximal disagreement roughly corresponds to a sparse cut
Polarization and Disagreement
Consider optimizing the polarization-disagreement index which simplifies
the problem to $\bar{\mathbf{s}}^T(I + L)^{-1}\bar{\mathbf{s}}$
The only relevant structure of the network that determines its robustness
to these adversarial perturbations is precisely determined by the second smallest eigenvalue
Defending the Network

Optimization Problem
Mixed Graph Objectives
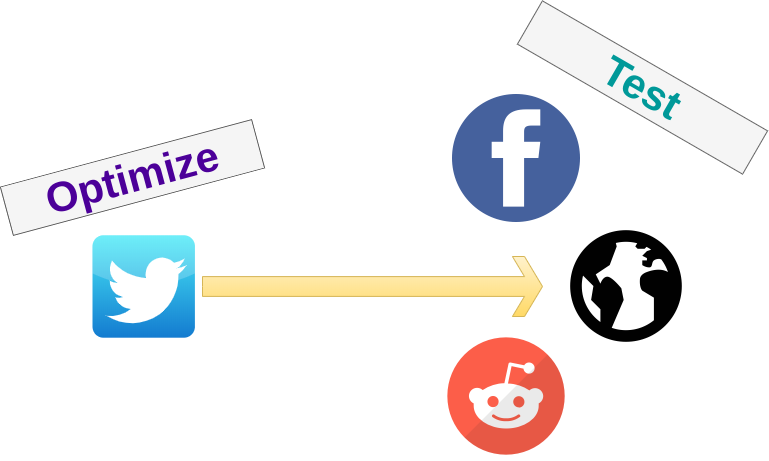
The authors show that having different graphs can actually reduce the adversary's power to induce disagreement
The relevant relationship that determines if an adversary gains extra power depends on spectral similarity between the two graphs
Optimization Problem
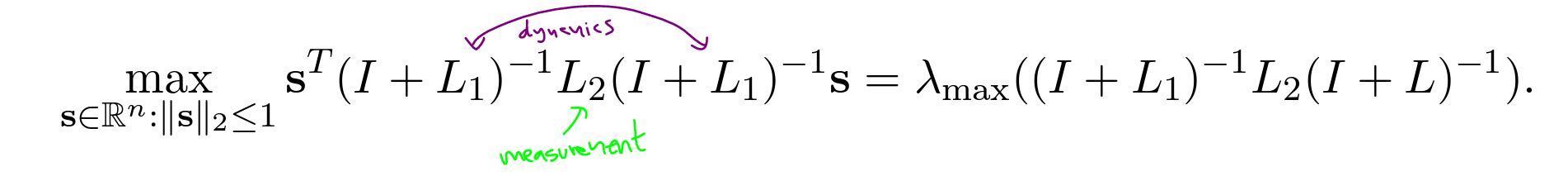
Summary of Results
The authors derive formal results that depend on $G_2$ being a regular graph or being a cycle (i.e., topology of the "real world" graph).
If $L_1 \approx L_2$ component-wise, then the optimization problem can be written in terms on the "real world" graph solely. The converse is not necessarily true, however.
Summary of Results
If $L_1$ and $L_2$ are spectrally misaligned then the largest eigenvalue of the mixed-graph objective problem is large.
If the opinion and disagreement graphs are misaligned on even one large cut, then the adversary will be able to induce disagreement far beyond what is possible in the single graph objective.
Conclusions
What's been achieved
Gain significant insights into the nature of graphs that are resilient to outside perturbations.Future Directions
Is it possible for an opinion dynamics model to fit into the $ENC$-$DEC$ setting from graph neural networks? (Many of them, benefit from an iterative algorithm.)
With mixed-graph objectives, is it possible to explain how disagreement can arise?
Consider different structural assumptions, such as, directed graphs, node attributes, dynamic graphs, etc.
What's missing in this paper
Experimental results (yet their theoretical arguments are very robust).
Contrast the presented conditions that guarantee perturbations with actual evaluation metrics of a supervised learning task (assuming we have a dataset labeled on opinion changes).
Discussion on cascading phenomena, which is presented on other literature and actually been explored recently as a relevant feature for rumour propagation.