Representation Learning on Graphs with Jumping Knowledge Networks
Keyulu Xu1, Chengtao Li1, Yonglong Tian1, Tomohiro Sonobe2, Ken-ichi Kawarabayashi2, Stefanie Jegelka11. Massachusetts Institute of Technology (MIT)
2. National Institute for Informatics, Tokyo;
2018
presented by Albert M Orozco Camacho
Motivation
Neighborhood aggregation turns out to be a crucial part of representation learning, due to the rise of graph neural networks.
Such procedure aims to extract high-level features from nodes via a message passing scheme.
Caveats of Traditional Aggregation Schemes
Usually, traditional GCNs show state-of-the-art performance only with a 2-layer model, while deeper models don't take advantage of accessing to more information.
Networks that exhibit a diversity in subgraph structures (such as node hubs) yield inconsistent learning of node relations by GCNs.
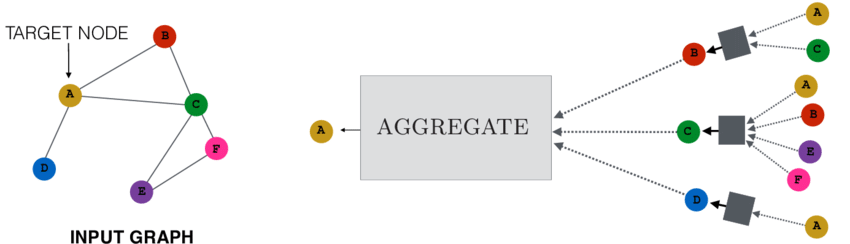
Neighborhood aggregation in GNNs
Changing Locality
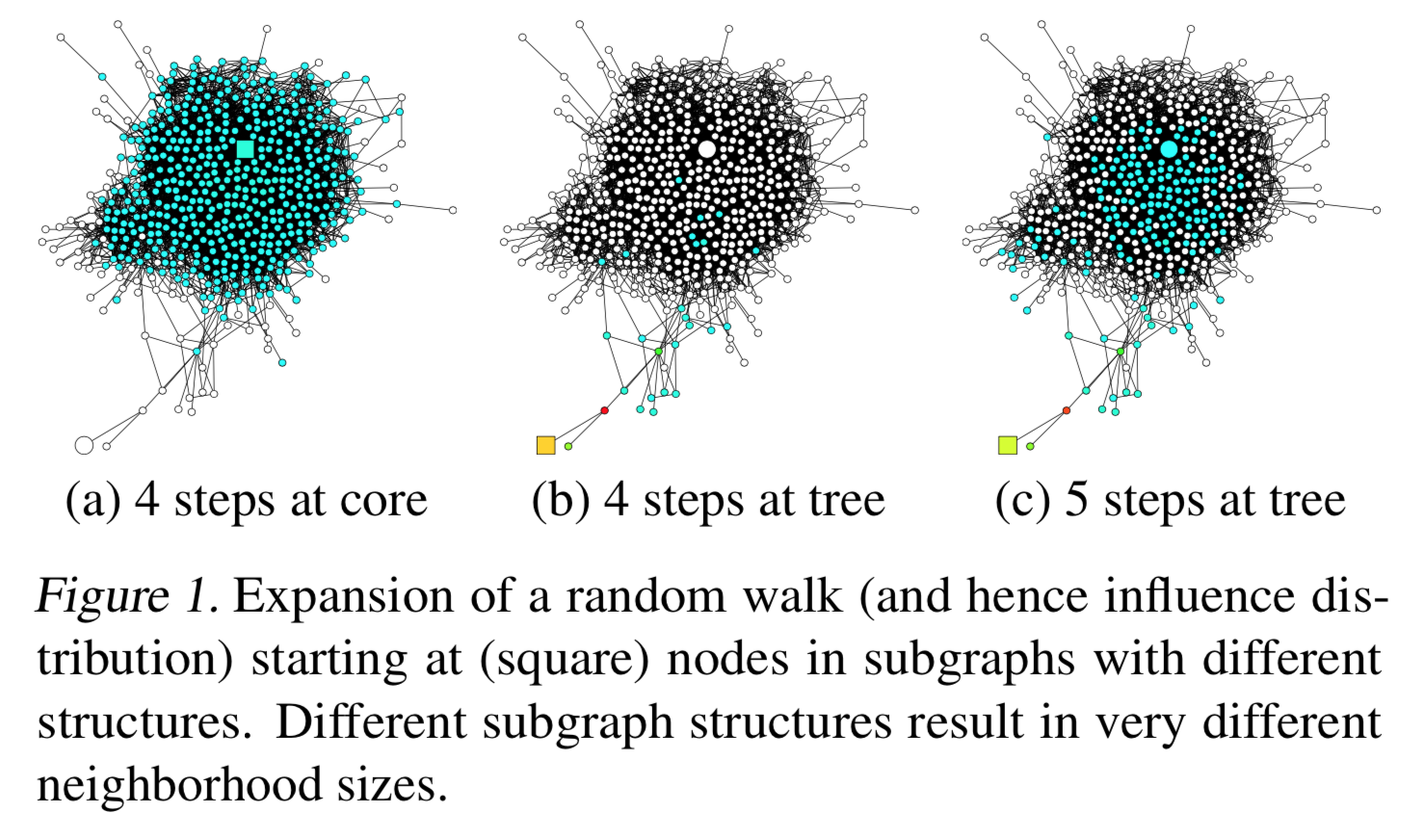
Influence distributions vs Random Walks
Background
Hidden Layer Update for a GNN
$$ h_v^{(l)} = \sigma\left(W_l \cdot \text{AGGREGATE}\left(\{h_u^{(l-1)}, \forall u \in \tilde{N}(v)\}\right)\right) $$Graph Convolutional Neural Networks
$$ h_v^{(l)} = \text{RELU}\left(W_l \cdot \sum_{u \in \tilde{N}(v)}(\deg(v)\deg(u))^{-\frac{1}{2}} h_u^{(l-1)}\right) $$
$$ h_v^{(l)} = \text{RELU}\left(W_l \cdot \frac{1}{\tilde{\deg}(v)} \sum_{u \in \tilde{N}(v)} h_u^{(l-1)}\right) $$
Neighborhood Aggregation with Skip Connections
$$ h_{N(v)}^{(l)} = \sigma\left(W_l \cdot \text{AGGREGATE}_N\left(\{h_u^{(l-1)}, \forall u \in N(v)\}\right)\right) $$$$ h_v^{(l)} = \text{COMBINE}\left(h_v^{(l-1)}, h_{N(v)}^{(l)}\right) $$
Influence Distributions
$$ I_x(y) = \frac{e^T \left[\frac{\partial h_x^{(k)}}{\partial h_y^{(0)}} e\right]}{\sum_{z \in V} e^T \frac{\partial h_x^{(k)}}{\partial h_z^{(0)}} e} $$where $e$ is an all-ones vector
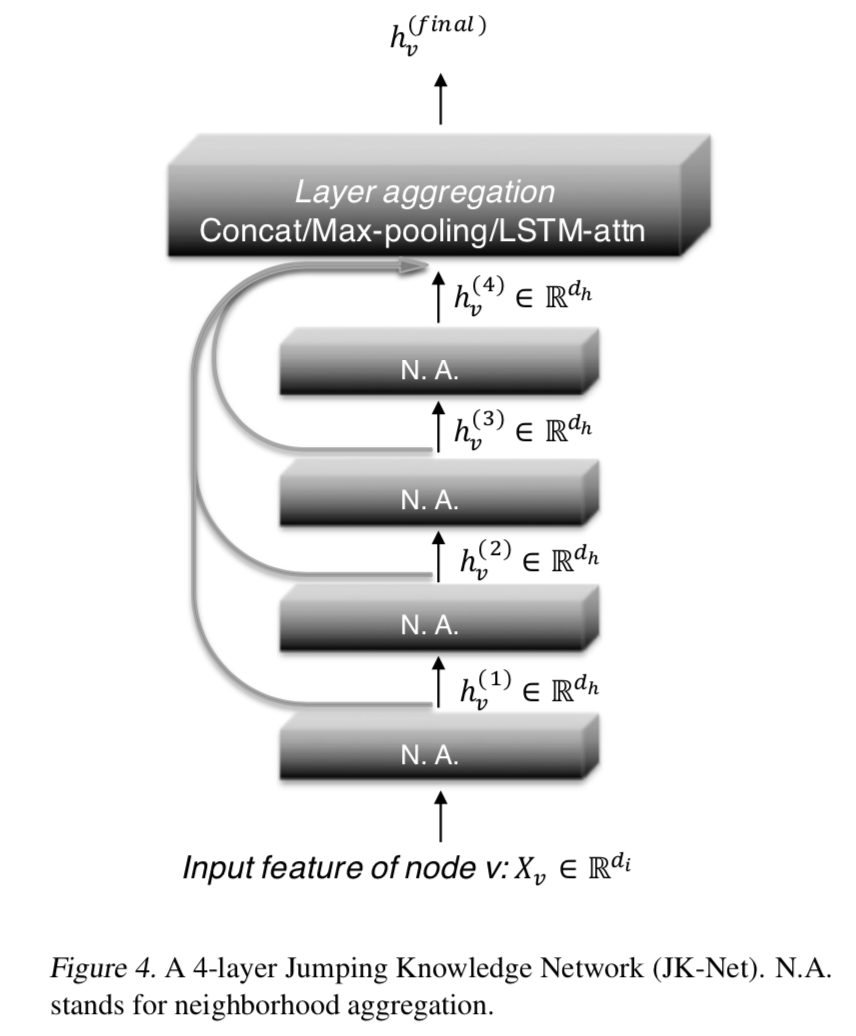
Jumping Knowledge Networks
The proposed aggregation scheme...
makes each layer increase the size of the influence distribution by aggregating
neighborhoods from the previous layer ⬆️;
combines, at the last layer, some of the previous layers' representations
independently for each node;
intermediate representations are said to jump to the last layer.
Aggregation Mechanisms
CONCATENATION
$$[h_v^{(1)},\ldots,h_v^{(k)}]$$
MAX-POOLING. Select the most informative layer for each feature coordinate.
LSTM-ATTENTION. Input $h_v^{(1)},\ldots,h_v^{(k)}$ into a bi-directional
LSTM to generate forward and backward features $f_v^{(l)}$ and $b_v^{(l)}$ for each
layer $l$; finally compute an attention score per each node by combining those
for each layer.
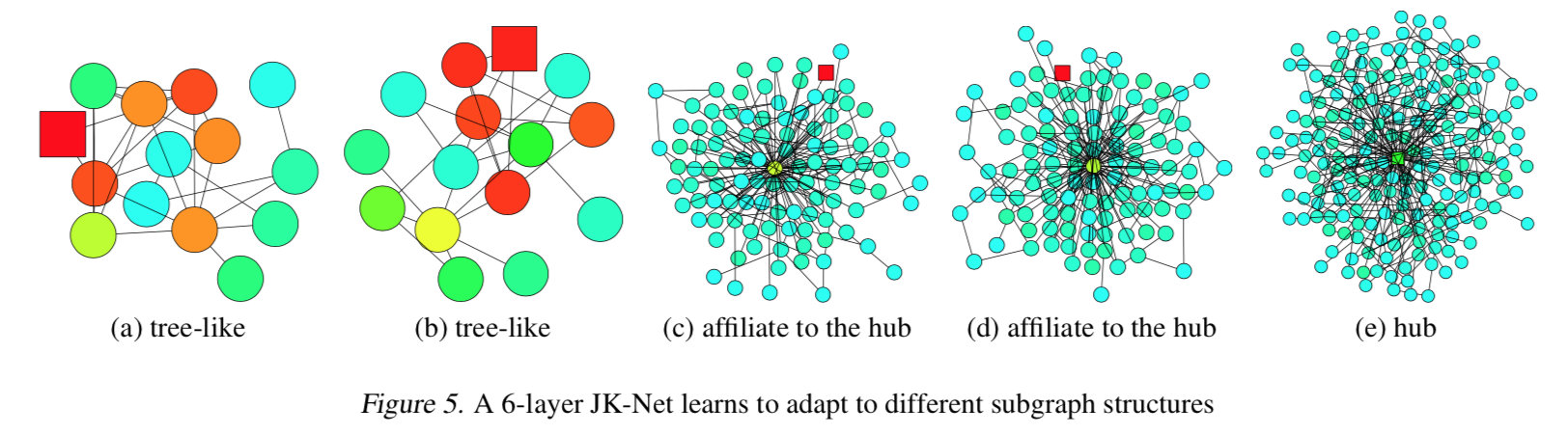
Proposition 1
Assume that paths of the same length in the computation graph are activated with the same probability.The influence score $I(x, y)$ for any $x, y \in V$ under a $k$-layer JK-Net with layer-wise max-pooling is equivalent in expectation to a mixture of $0,\ldots,k$-step random walk distributions on $\tilde{G}$ at $y$ starting at $x$, the coefficients of which depend on the values of the layer features $h_x^{(l)}$.
Experiments
Datasets

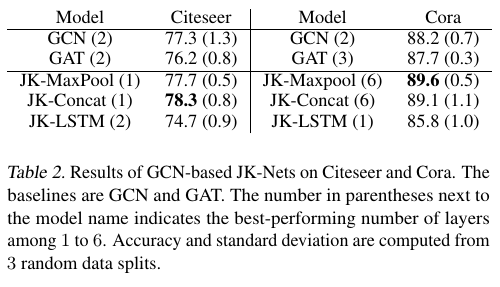

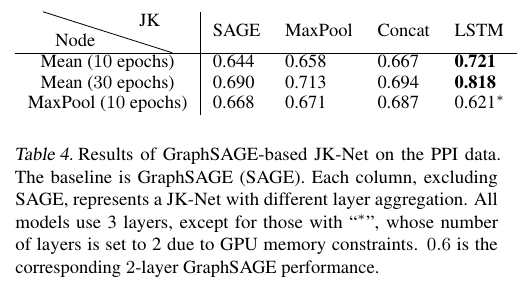
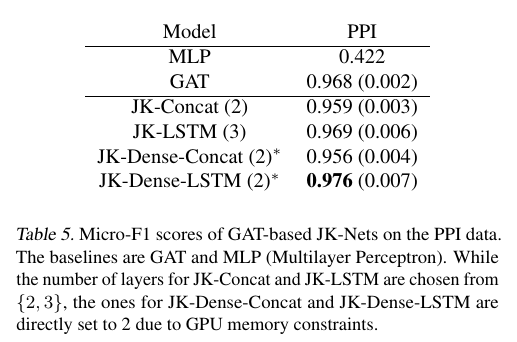
Conclusion

Goal: Provide a representation learning scheme that can generalize better on diverse variety of network structure, than the one proposed for GCN's
Problem: Denser subgraphs may cause aggregation algorithms to converge in expectation to biased random walks. ☹
Solution: JK-Nets aggregate and leverage information from more than one hidden layers.😁
JK-Nets with the LSTM-attention aggregators outperform the non-adaptive models GraphSAGE, GAT and JK-Nets with concatenation aggregators.
https://github.com/ShinKyuY/Representation_Learning_on_Graphs_with_Jumping_Knowledge_Networks
Future Work
Exploring other layer aggregators and studying the effect of the combination of various layer-wise and node-wise aggregators on different types of graph structures.
How can sequence modelling by itself impact the task of layer aggregation?
Are there smarter ways to keep track of node/community correlations within a network?